Nonlinear Methods

Nonlinear Methods#

ใน tutorial ก่อนหน้า เราได้เห็นถึงความสามารถของเทคนิค PCA ในการ transform ข้อมูล รวมถึงความสามารถในการลดมิติลงอย่างมีประสิทธิภาพ แต่ก็ยังมีข้อมูลอีกจำนวนมากที่ไม่เหมาะกับเทคนิค PCA

Slides: Nonlinear Dimensionality Reduction

ตัวอย่างแรก#

เราจะลองใช้ PCA กับข้อมูลชุดใหม่ที่ถูกสร้างไว้ตาม code ด้านล่าง

import sys
import numpy as np
from sklearn.decomposition import PCA
from numpy.random import multivariate_normal
import matplotlib.pyplot as plt
from matplotlib import colors

np.random.seed(42) # ตั้งค่า random seed เอาไว้ เพื่อให้การรันโค้ดนี้ได้ผลเหมือนเดิม

num_points = 100

# สร้างจุดขึ้นมาเป็นจำนวน num_points จุด ซึ่งมาจาก multi-variate normal distribution สำหรับ class 1
data_class1 = multivariate_normal(mean=[-0.5, -0.5], cov=[[3, -1], [-1, 0.5]], size=num_points)

# สร้างจุดขึ้นมาเป็นจำนวน num_points จุด ซึ่งมาจาก multi-variate normal distribution สำหรับ class 2
data_class2 = multivariate_normal(mean=[0.5, 0.5], cov=[[3, -1], [-1, 0.5]], size=num_points)

# รวมข้อมูลจากทั้ง 2 class มาเก็บไว้ในตัวแปร data และเก็บ label (class) เอาไว้ในตัวแปรชื่อ labels
data = np.concatenate((data_class1, data_class2), axis=0)
labels = np.zeros(num_points*2, )
labels[num_points:] = 1

# เตรียมแสดงผล
x_disp = [-6.0, 6.0] # ค่าต่ำสูงและสูงสุดของ x สำหรับแสดงผล
y_disp = [-6.0, 6.0] # ค่าต่ำสูงและสูงสุดของ y สำหรับแสดงผล

# ใช้สีน้ำเงินสำหรับแสดงจุดข้อมูลที่มาจาก class 1 (label=0) และใช้สีแดงสำหรับแสดงจุดข้อมูลที่มาจาก class 2 (label=1)
cmap = colors.ListedColormap(["blue","red"])

fig, ax = plt.subplots()

# แสดงรูปข้อมูลเริ่มต้น
ax.scatter(data[:, 0], data[:, 1], c=labels, cmap=cmap)
ax.plot([0, 0], y_disp, c="grey") # Plot แกน y
ax.plot(x_disp, [0, 0], c="grey") # Plot แกน x
ax.set(xlabel='x', ylabel='y')
ax.set_title("Original data")
fig.show()

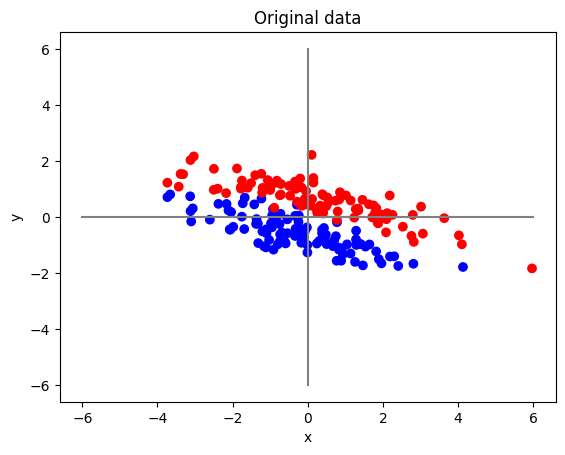
../../_images/d17a59a121fa7e4d24c8c65d1f3d57021427ea4b68c5cf38e5e8eb47b07da8ab.png

ต่อมาเราจะลองใช้เทคนิค PCA เพื่อลดจำนวนมิติของข้อมูลนี้กัน

# สร้าง PCA สำหรับตัวอย่างนี้เราจะไม่ whiten ข้อมูลของเรา โดยการกำหนด whiten=False แต่ในการใช้งานจริง การทำ whitening เป็นสิ่งที่ค่อนข้างมีความสำคัญมาก
model_PCA = PCA(n_components=2, whiten=False)

# การทำ PCA เราไม่ใช้ข้อมูลว่าจุดข้อมูลไหนมาจาก class ไหนเลย (หรืออาจมองว่า PCA มองทุกจุดเป็นสีเดียวกันก็ได้)
model_PCA.fit(data)

# ดึงเอา principal component (pc) ออกมา
pc1 = model_PCA.components_[0]
pc2 = model_PCA.components_[1]

# คำนวณหาความชันของเส้นตรงที่วิ่งผ่านจุด (0,0) และว่ิงไปในทิศทางเดียวกับ principal component -> y = m*x
m_pc1 = pc1[1]/pc1[0]
m_pc2 = pc2[1]/pc2[0]

# คำนวณพิกัดใหม่ของทุกจุดข้อมูล
data_pca = model_PCA.transform(data)

fig, ax = plt.subplots(1, 3, figsize=(18, 6))

# แสดงรูปข้อมูลเริ่มต้น
ax[0].scatter(data[:, 0], data[:, 1], c=labels, cmap=cmap)
ax[0].plot([0, 0], y_disp, c="grey") # Plot แกน y
ax[0].plot(x_disp, [0, 0], c="grey") # Plot แกน x
ax[0].set(xlabel='x', ylabel='y')
ax[0].set_title("Original data")

# แสดงรูปข้อมูลเริ่มต้นโดยมี principal component ทั้ง 2 อันแสดงอยู่ด้วย
ax[1].scatter(data[:, 0], data[:, 1], c=labels, cmap=cmap)
ax[1].plot(x_disp, [m_pc1*x_disp[0], m_pc1*x_disp[1]], c="m", alpha=1) # แสดง pc1 โดยใช้สมการ y = m1*x
ax[1].plot(x_disp, [m_pc2*x_disp[0], m_pc2*x_disp[1]], c="m", alpha=0.3) # แสดง pc2 โดยใช้สมการ y = m2*x
ax[1].set(xlabel='x', ylabel='y')
ax[1].set_title("Original data with the principal components shown")

# แสดงข้อมูลหลังถูก transform ด้วย PCA (หน้าตาจะเหมือนกับรูปที่แล้ว แต่มีการหมุนแกน)
ax[2].scatter(data_pca[:, 0], data_pca[:, 1], c=labels, cmap=cmap)
ax[2].plot(x_disp, [0, 0], c="m", alpha=1) # แสดงผลโดยการหมุนแกน pc1 ให้มาอยู่ที่ตำแหน่งแกน x
ax[2].plot([0, 0], y_disp, c="m", alpha=0.3) # แสดงผลโดยการหมุนแกน pc2 ให้มาอยู่ที่ตำแหน่งแกน y
ax[2].set(xlabel=f"PC1 score (explained var = {model_PCA.explained_variance_ratio_[0]*100: 0.2f}%)",
          ylabel=f"PC2 score (explained var = {model_PCA.explained_variance_ratio_[1]*100: 0.2f}%)")
ax[2].set_title("PCA-tranformed data")

plt.setp(ax, xlim=x_disp, ylim=y_disp)
plt.show()


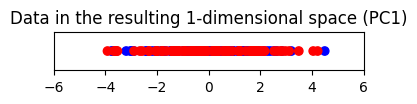
# Plot ข้อมูลที่ลดมิติโดยการตัดแกน PC2 ทิ้งไป
plt.figure(figsize=(4, 0.5))
plt.scatter(data_pca[:, 0], np.zeros_like(data_pca[:, 0]), c=labels, cmap=cmap)
ax[2].plot(x_disp, [0, 0], c="m", alpha=1) # แสดงผลโดยการหมุนแกน pc1 ให้มาอยู่ที่ตำแหน่งแกน x
plt.xlim(x_disp)
plt.ylim(-0.5, 0.5)
plt.title("Data in the resulting 1-dimensional space (PC1)")
plt.yticks([])

# Plot ข้อมูลที่ลดมิติโดยการตัดแกน PC1 ทิ้งไป
plt.figure(figsize=(4, 0.5))
plt.scatter(data_pca[:, 1], np.zeros_like(data_pca[:, 1]), c=labels, cmap=cmap)
ax[2].plot(x_disp, [0, 0], c="m", alpha=0.3) # แสดงผลโดยการหมุนแกน pc2 ให้มาอยู่ที่ตำแหน่งแกน x
plt.xlim(x_disp)
plt.ylim(-0.5, 0.5)
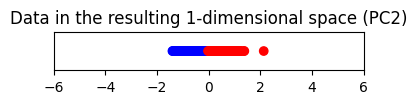
plt.title("Data in the resulting 1-dimensional space (PC2)")
plt.yticks([])
plt.show()

print(f"% variance captured by PC1 = {model_PCA.explained_variance_ratio_[0]*100: 0.2f}")
print(f"% variance captured by PC2 = {model_PCA.explained_variance_ratio_[1]*100: 0.2f}")

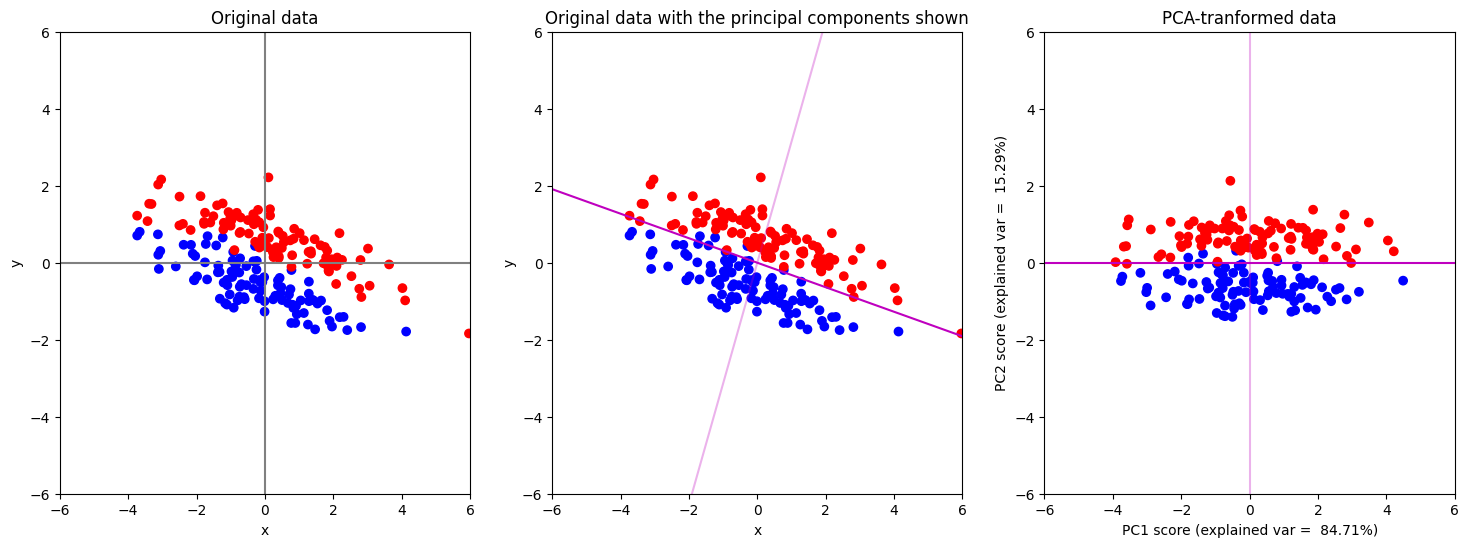
../../_images/adf1033928abd41bdc3c9593933190ee06d9dc3834cd55d9c4a9638933f8c038.png

../../_images/401bf0835dd7595847743679acddc45235d6bdd7b037da30b42f65465a4468b4.png

../../_images/b521e914b5863b6edf4243d5785bd25ba4a116a6932d63c9cfaecf4c8badf868.png

% variance captured by PC1 =  84.71
% variance captured by PC2 =  15.29

เทคนิค PCA เลือกแกน PC1 ที่อธิบายการกระจายตัวในข้อมูลสูง (มากกว่า 80%) วัดด้วยค่า variance แต่เมื่อลดมิติลงมาแล้วพบว่า PC1 score ของทั้งสอง classes มาซ้อนทับกัน

แต่ถ้าเราลดมิติลงโดยการเก็บ PC2 ไว้แทน จะพบว่าข้อมูลจากทั้งสอง class จะแยกออกจากกันได้ดีกว่า

ในข้อมูลชุดนี้จะเห็นได้ว่าแกนที่อธิบาย variance ได้สูงกว่า ก็อาจจะไม่ได้เป็นแกนที่จะทำให้ข้อมูลจากต่าง class กระจายตัวออกจากกันได้ดีกว่าเสมอไป

ในกรณีที่เราต้องการลดจำนวนมิติโดยต้องการให้ข้อมูลจากต่าง class กระจายตัวออกจากกัน เราอาจจะต้องไปทดลองใช้เทคนิคประเภท supervised learning เช่น linear discriminant analysis (LDA) แทน ซึ่งเทคนิคเหล่านี้สามารถนำเอาข้อมูล labels (ข้อมูลไหนมาจาก class อะไร) มาใช้ในกระบวนการลดจำนวนมิติได้

ตัวอย่างที่ 2#

เรามาลองดูอีกตัวอย่างหนึ่ง ซึ่งเป็น dataset ที่เป็นรูปภาพตัวเลข 0 ถึง 9

ที่มาของโค้ดสำหรับ download ชุดข้อมูล: https://umap-learn.readthedocs.io/en/latest/basic_usage.html#digits-data

from sklearn.datasets import load_digits
digits = load_digits()

ดูตัวอย่างภาพ

# เอาข้อมูลมาเก็บไว้ใน variables
images_flatten = digits.data
labels = digits.target

num_classes = len(list(set(labels)))

print(f"Images: {images_flatten.shape}")
print(f"Labels: {labels.shape}")
print(f"There are {images_flatten.shape[0]} samples.")
print(f"There are {num_classes} classes.")

# ดูตัวอย่างภาพ
plt.figure()

for count, idx_img in enumerate(range(0, 1500, 100)):
    plt.subplot(1, 15, count+1)
    plt.imshow(np.reshape(images_flatten[idx_img, :], (8, 8)))
    plt.axis('off')
    plt.gray()

Images: (1797, 64)
Labels: (1797,)
There are 1797 samples.
There are 10 classes.

../../_images/465408156b4ae3141b3dad8cb7a6125987e364de23dd74b2d0d97877abb7c3ea.png

เรียกใช้ sklearn.decomposition.PCA เหมือนในตัวอย่างก่อนหน้า แต่เราจะลองให้ PCA หาแกนมาเป็นจำนวนเท่ากับจำนวนมิติตั้งต้นเลย (64 แกน)

ในที่นี้จะเห็นได้ว่า PCA แปลงข้อมูลโดยไม่ได้ใช้ข้อมูล labels เลย

n_components = images_flatten.shape[-1]
model_PCA = PCA(n_components=n_components, whiten=True, random_state=20)
images_PCA = model_PCA.fit_transform(images_flatten)

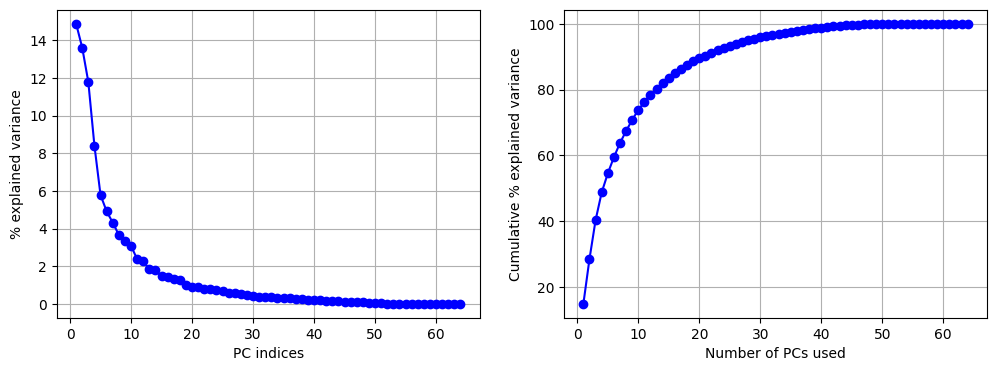
ลองดูว่าแต่ละแกนที่ PCA หามาสามารถอธิบาย variance ได้เท่าไหร่กันบ้าง

fig, ax = plt.subplots(1, 2, figsize=(12, 4))

# Plot ดูว่า PC แต่ละตัวสามารถอธิบาย variance ได้กี่ %
ax[0].plot(np.arange(1, n_components+1), model_PCA.explained_variance_ratio_*100, c='b', marker='o')
ax[0].set(xlabel='PC indices', ylabel='% explained variance')
ax[0].grid(True)

# Plot ดูว่าการเอา PC มารวมกันหลาย ๆ ตัว (เริ่มจากตัวแรก เรียงไป) จะสามารถอธิบาย variance รวมได้กี่ %
cumulative_exp_var = np.cumsum(model_PCA.explained_variance_ratio_*100)
ax[1].plot(np.arange(1, n_components+1), cumulative_exp_var, c='b', marker='o')
ax[1].set(xlabel='Number of PCs used', ylabel='Cumulative % explained variance')
ax[1].grid(True)

plt.show()

print(f"% variance captured by PC1 = {model_PCA.explained_variance_ratio_[0]*100: 0.2f}")
print(f"% variance captured by PC2 = {model_PCA.explained_variance_ratio_[1]*100: 0.2f}")
print(f" It takes {np.argwhere(cumulative_exp_var>95)[0][0] + 1} top PCs to be able to explain 95% of the variance")

../../_images/6c906ac15c3cf4fb6993b5e7be335a1d83a897bf5c9a764199ee419cdf22d2b0.png

% variance captured by PC1 =  14.89
% variance captured by PC2 =  13.62
 It takes 29 top PCs to be able to explain 95% of the variance

ลองนำผลลัพธ์ที่ได้มา plot ดูว่าข้อมูลจากแต่ละ class มีการกระจายตัวหรือกระจุกตัวกันอย่างไร โดยในที่นี้เราจะใช้สีที่แตกต่างกันเพื่อแสดงให้ดูว่าข้อมูลจาก class ไหน อยู่บริเวณใดใน space 2 มิติ

fig, ax = plt.subplots(figsize=(6, 4))
sp = ax.scatter(images_PCA[:, 0], images_PCA[:, 1], c=labels, cmap='rainbow', alpha=0.5)
ax.set_aspect('equal', 'datalim')
ax.set(xlabel='PC1 score', ylabel='PC2 score')
ax.set_title('Data in the PCA-transformed space')
fig.colorbar(sp, ax=ax, boundaries=np.arange(num_classes+1)-0.5).set_ticks(np.arange(num_classes))
plt.show()

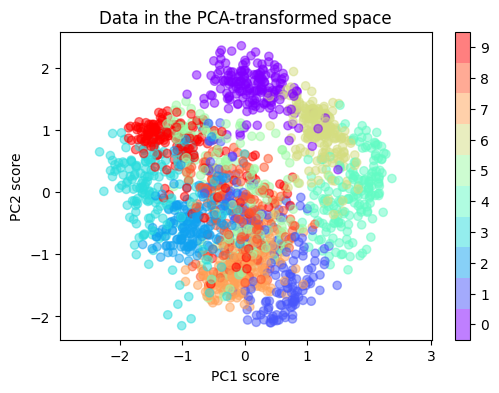
../../_images/97124f15f879893e15b257070f57a49e274ce6220aae44688e42cb98a143029d.png

ข้อมูลที่ถูกลดจำนวนมิติลงมาเหลือ 2 มิติด้วย PCA มีข้อสังเกตดังนี้

ข้อมูลที่มาจาก class เดียวกัน (ตัวเลขเดียวกัน) จะเกาะกลุ่มกัน เช่น กลุ่มของ ภาพเลข 0 (สีม่วง)
ข้อมูลที่มาจากคนละ class มีการกระจายตัวออกจากกันบ้างในบาง class เช่น กลุ่มเลข 0 กลุ่มเลข 6 และ กลุ่มเลข 4 ซ้อนทับกันเพียงเล็กน้อย
ข้อมูลจาก class ที่เหลือ ซ้อนทับกันมาก โดยเฉพาะ กลุ่มเลข 5 และเลข 9

ถ้าหากว่าผู้เรียนมีเวลาว่าง อยากให้ลองไปหาวิธี visualize ดูว่าบริเวณจุดที่ซ้อนทับกันเยอะ ๆ มีข้อมูลก่อนลดมิติหน้าตาคล้ายคลึงกันหรือไม่ (เป็นภาพ 8 x 8 มิติ ที่มีความคล้ายคลึงกันหรือไม่)

หมายเหตุ ขอย้ำอีกครั้งว่า PCA ไม่ได้ใช้ข้อมูล labels ในการลดจำนวนมิติเลย

เราอาจจะเคยเรียนมาในคณิตศาสตร์ระดับมัธยมว่าเราสามารถคำนวณระยะห่างระหว่างจุด 2 จุด \((x_1, y_1)\) และ \((x_2, y_2)\) ได้ด้วยสูตร \(d = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}\) ซึ่งค่า \(d\) ที่เราคำนวณได้ ก็คือความยาวของเส้นตรงที่ลากเชื่อม จุด \((x_1, y_1)\) และ \((x_2, y_2)\) เข้าด้วยกัน การวัดระยะห่างแบบเส้นตรงในลักษณะนี้มีชื่อทางเทคนิคว่า Euclidean distance (ใน 2 มิติ)

code ใน cell ถัดมาจะแสดง Euclidean distance ระหว่างจุดสองคู่

คู่แรกจะเป็นตัวอย่างจุด 2 จุดที่อยู่ใน class เดียวกัน โดยเราสามารถแสดง Euclidean distance ระหว่างจุดทั้งสองด้วยเส้นตรงสีส้ม
คู่ที่สองจะเป็นตัวอย่างจุด 2 จุดที่มาจากคนละ class โดยเราสามารถแสดง Euclidean distance ระหว่างจุดทั้งสองด้วยเส้นตรงสีเขียว

# Code ในส่วนนี้เป็น code ที่ปรับแก้มาจาก tutorial ที่แล้วเพียงเล็กน้อย ผู้เรียนไม่ต้องกังวลเกี่ยวกับรายละเอียดของ code ใน cell นี้ ซึ่งจะใช้ในการอธิบาย concept เท่านั้น ไม่ได้คำนึงถึงการเขียนให้ optimize performance

def euclidean_distance_PCA_example():
    num_points = 20

    # สร้างจุดขึ้นมาเป็นจำนวน num_points จุด ซึ่งมาจาก multi-variate normal distribution สำหรับ class 1
    data_class1 = multivariate_normal(mean=[-2, -2], cov=[[1.5, 1], [1, 1]], size=num_points)

    # สร้างจุดขึ้นมาเป็นจำนวน num_points จุด ซึ่งมาจาก multi-variate normal distribution สำหรับ class 2
    data_class2 = multivariate_normal(mean=[2, 2], cov=[[1.5, 1], [1, 1]], size=num_points)

    # รวมข้อมูลจากทั้ง 2 class มาเก็บไว้ในตัวแปร data และเก็บ label (class) เอาไว้ในตัวแปรชื่อ labels
    data = np.concatenate((data_class1, data_class2), axis=0)
    labels = np.zeros(num_points*2, )
    labels[num_points:] = 1

    # สร้าง PCA สำหรับตัวอย่างนี้เราจะไม่ whiten ข้อมูลของเรา โดยการกำหนด whiten=False แต่ในการใช้งานจริง การทำ whitening เป็นสิ่งที่ค่อนข้างมีความสำคัญมาก
    model_PCA = PCA(n_components=2, whiten=False)

    # การทำ PCA เราไม่ใช้ข้อมูลว่าจุดข้อมูลไหนมาจาก class ไหนเลย (หรืออาจมองว่า PCA มองทุกจุดเป็นสีเดียวกันก็ได้)
    model_PCA.fit(data)

    # คำนวณพิกัดใหม่ของทุกจุดข้อมูล
    data_pca = model_PCA.transform(data)

    # เตรียมแสดงผล
    x_disp = [-6.0, 6.0] # ค่าต่ำสูงและสูงสุดของ x สำหรับแสดงผล
    y_disp = [-6.0, 6.0] # ค่าต่ำสูงและสูงสุดของ y สำหรับแสดงผล

    # ใช้สีน้ำเงินสำหรับแสดงจุดข้อมูลที่มาจาก class 1 (label=0) และใช้สีแดงสำหรับแสดงจุดข้อมูลที่มาจาก class 2 (label=1)
    cmap = colors.ListedColormap(["blue","red"])

    fig, ax = plt.subplots(1, 2, figsize=(12, 6))

    # แสดงรูปข้อมูลเริ่มต้น
    ax[0].scatter(data[:, 0], data[:, 1], c=labels, cmap=cmap)
    ax[0].plot([0, 0], y_disp, c="grey") # Plot แกน y
    ax[0].plot(x_disp, [0, 0], c="grey") # Plot แกน x
    ax[0].plot(data[:2, 0], data[:2, 1], c='darkorange') # Plot จุดเชื่อมระหว่างจุด 1 คู่จาก class เดียวกัน
    ax[0].plot(data[num_points-1:num_points+1, 0], data[num_points-1:num_points+1, 1], c='green') # Plot จุดเชื่อมระหว่างจุด 1 คู่ การคนละ class
    ax[0].set(xlabel='x', ylabel='y')
    ax[0].set_title("Original data")


    # แสดงข้อมูลหลังถูก transform ด้วย PCA (หน้าตาจะเหมือนกับรูปที่แล้ว แต่มีการหมุนแกน)
    ax[1].scatter(data_pca[:, 0], data_pca[:, 1], c=labels, cmap=cmap)
    ax[1].plot(x_disp, [0, 0], c="m", alpha=1) # แสดงผลโดยการหมุนแกน pc1 ให้มาอยู่ที่ตำแหน่งแกน x
    ax[1].plot([0, 0], y_disp, c="m", alpha=0.3) # แสดงผลโดยการหมุนแกน pc2 ให้มาอยู่ที่ตำแหน่งแกน y
    ax[1].plot(data_pca[:2, 0], data_pca[:2, 1], c='darkorange') # Plot จุดเชื่อมระหว่างจุด 1 คู่จาก class เดียวกัน
    ax[1].plot(data_pca[num_points-1:num_points+1, 0], data_pca[num_points-1:num_points+1, 1], c='green') # Plot จุดเชื่อมระหว่างจุด 1 คู่ การคนละ class
    ax[1].set(xlabel=f"PC1 score (explained var = {model_PCA.explained_variance_ratio_[0]*100: 0.2f}%)",
              ylabel=f"PC2 score (explained var = {model_PCA.explained_variance_ratio_[1]*100: 0.2f}%)")
    ax[1].set_title("PCA-tranformed data")

    plt.setp(ax, xlim=x_disp, ylim=y_disp)
    plt.show()

euclidean_distance_PCA_example()

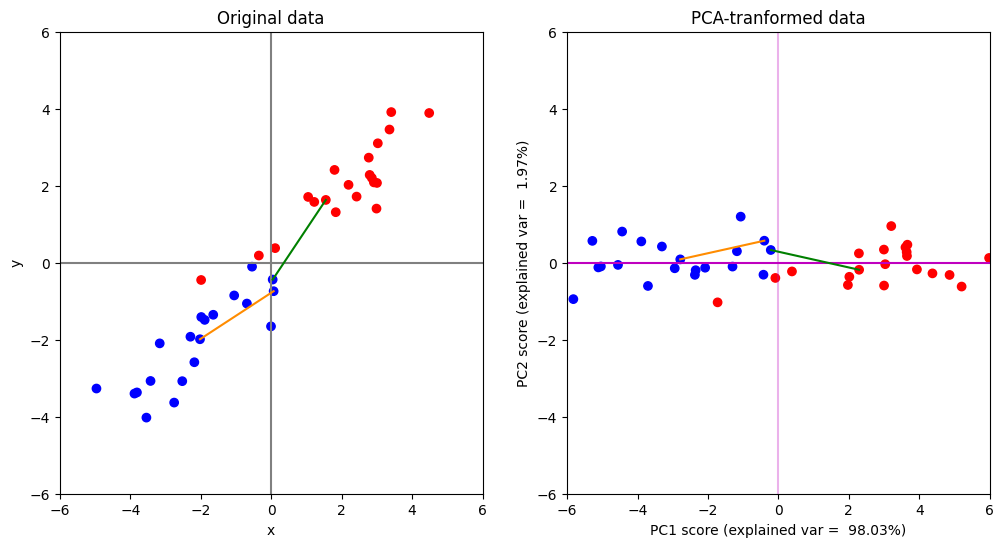
../../_images/545af7a1d07ce4c71aa71df7b4daf3e0d67253f63ae38b9f65b52e1f63231d5e.png

จากตัวอย่างนี้จะเห็นได้ว่าการหมุนแกนโดย PCA จะไม่เปลี่ยนค่า Euclidean distance ระหว่างคู่จุดใด ๆ ในข้อมูลเลย (เส้นตรงสีส้มในภาพด้านซ้ายมีขนาดเท่ากับเส้นตรงสีส้มในภาพด้านขวา และ เส้นตรงสีเขียวในภาพด้านซายมีขนาดเท่ากับเส้นตรงสีเขียวในภาพด้านขวาทุกประการ)

หรือพูดอีกอย่างนึงก็คือ PCA รักษา Euclidean distance ซึ่งแปลว่าสมมติฐานที่สำคัญมาก ๆ ของ PCA ก็คือ การวัดระยะระหว่างจุดข้อมูลด้วย Euclidean distance เป็นสิ่งที่มีความเหมาะสมมากที่สุดสำหรับโจทย์ข้อนี้

PCA เป็นเทคนิคที่ใช้งานง่ายและได้ผลที่ดีในหลาย ๆ กรณี ทำให้เป็นเทคนิคที่มักจะถูกนำไปใช้เป็นเทคนิคแรกเวลาเราต้องการลดจำนวนมิติของข้อมูล แต่ PCA ก็มีข้อกำจัดหลายประการ เช่น

เป็นเทคนิคประเภท linear ซึ่งทำให้ได้ผลไม่ค่อยดีเวลาเจอข้อมูลที่มีความซับซ้อนและมีความเป็น nonlinearity สูงมาก
เป็นเทคนิคที่อ้างอิงการวัดระยะห่างด้วย Euclidean distance เท่านั้น ซึ่งเป็นการวัดที่เราอาจจะคุ้นเคยมากที่สุด แต่ถ้าเกิดว่าการวัดระยะห่างด้วย Euclidean distance นั้นไม่มีความเหมาะสม PCA ก็จะเป็นเทคนิคที่ไม่ค่อยเหมาะนัก

ในหลายสถานการณ์ การวัดระยะห่างระหว่างจุด 2 จุด อาจต้องใช้ distance ประเภทอื่น นอกเหนือไปจาก Euclidean distance ที่วัดระยะห่างเป็นเส้นตรง

แหล่งที่มาของภาพ: 9 Distance Measures in Data Science

จากภาพข้างบน จะเห็นได้ว่ามีวิธีการวัดความเหมือน ความคล้าย ระยะห่างระหว่างของ 2 สิ่งหลายวิธี ซึ่งแต่ละอันก็เหมาะสมกับโจทย์หรือสถานการณ์ที่แตกต่างกัน เช่น

ถ้าเราต้องการวัดค่าความเหมือนของจุด 2 จุดด้วยมุมระหว่างจุดทั้งสอง เราอาจจะเลือกใช้ cosine similarity ได้
ถ้าเกิดว่าเรามีจุดข้อมูลที่เป็น set 2 อัน แล้วเราต้องการจะดูว่าทั้งสองอันมันเหมือนกันแค่ไหน เราก็สามารถเลือกใช้ Jaccard index ในการวัดได้ เช่น เวลาเราตรวจข้อสอบเข้ากิจกรรม Brain Code Camp ที่เป็นแบบปรนัย (multiple choices) ที่เราให้ผู้สอบตอบทุกตัวเลือกที่มีความถูกต้อง เราก็สามารถใช้ Jaccard index เป็นตัววัดความเหมือนระหว่าง set คำตอบของผู้สอบกับ set เฉลยของผู้สอนได้

Nonlinear methods#

ในส่วนที่เหลือเราจะลองใช้เทคนิคประเภท nonlinear ดูว่าจะสามารถลดจำนวนมิติได้ดีกว่า PCA ซึ่งเป็นเทคนิคประเภท linear สำหรับข้อมูลชุดนี้ได้หรือไม่

เทคนิคประเภท nonlinear มีหลายประเภท เช่น Multidimensional scaling (MDS), t-distributed Stochastic Neighbor Embedding (t-SNE), Uniform Manifold Approximation and Projection (UMAP) และ PHATE ซึ่งหลายเทคนิคในนี้สามารถรองรับการวัดระยะระหว่างจุดข้อมูลได้หลายรูปแบบ ไม่จำเป็นต้องเป็น Euclidean distance ก็ได้

หมายเหตุ เนื่องจากผู้เรียนจำนวนหนึ่งอาจไม่มีพื้นฐานทางคณิตศาสตร์ที่เพียงพอต่อการเข้าใจเทคนิค nonlinear หลายประเภทที่ถูกใช้อย่างกว้างขวาง ใน tutorial นี้เราจะเน้นการนำเอาเทคนิคบางอันไปทดลองใช้งานมากกว่า

เรามาลองใช้ UMAP กัน

# ติดตั้ง UMAP
!{sys.executable} -m pip install umap-learn

Looking in indexes: https://pypi.org/simple, https://us-python.pkg.dev/colab-wheels/public/simple/
Requirement already satisfied: umap-learn in /usr/local/lib/python3.10/dist-packages (0.5.3)
Requirement already satisfied: numpy>=1.17 in /usr/local/lib/python3.10/dist-packages (from umap-learn) (1.22.4)
Requirement already satisfied: scikit-learn>=0.22 in /usr/local/lib/python3.10/dist-packages (from umap-learn) (1.2.2)
Requirement already satisfied: scipy>=1.0 in /usr/local/lib/python3.10/dist-packages (from umap-learn) (1.10.1)
Requirement already satisfied: numba>=0.49 in /usr/local/lib/python3.10/dist-packages (from umap-learn) (0.56.4)
Requirement already satisfied: pynndescent>=0.5 in /usr/local/lib/python3.10/dist-packages (from umap-learn) (0.5.10)
Requirement already satisfied: tqdm in /usr/local/lib/python3.10/dist-packages (from umap-learn) (4.65.0)
Requirement already satisfied: llvmlite<0.40,>=0.39.0dev0 in /usr/local/lib/python3.10/dist-packages (from numba>=0.49->umap-learn) (0.39.1)
Requirement already satisfied: setuptools in /usr/local/lib/python3.10/dist-packages (from numba>=0.49->umap-learn) (67.7.2)
Requirement already satisfied: joblib>=0.11 in /usr/local/lib/python3.10/dist-packages (from pynndescent>=0.5->umap-learn) (1.2.0)
Requirement already satisfied: threadpoolctl>=2.0.0 in /usr/local/lib/python3.10/dist-packages (from scikit-learn>=0.22->umap-learn) (3.1.0)

Import umap มาใช้งาน

import umap

สร้างและใช้ UMAP ในการลดจำนวนมิติของข้อมูล โดยที่ไม่ได้ใช้ข้อมูล labels สำหรับลดจำนวนมิติลง

หมายเหตุ UMAP มี parameters ที่เราต้องลองปรับค่าดู เช่น n_neighbors, min_dist, n_components และ metric ซึ่งเราสามารถไปลองศึกษาเพิ่มเติมได้จาก https://umap-learn.readthedocs.io/en/latest/parameters.html#min-dist

model_umap = umap.UMAP(n_components=2, n_neighbors=15, metric='euclidean', min_dist=0.1, random_state=42)

images_UMAP = model_umap.fit_transform(images_flatten)
print(images_UMAP.shape)

(1797, 2)

Plot ผลที่ได้จาก UMAP มาเทียบกับ PCA โดยในที่นี้เราจะใช้สีที่แตกต่างกันเพื่อแสดงให้ดูว่าข้อมูลจาก class ไหน อยู่บริเวณใดใน space 2 มิติ

fig, ax = plt.subplots(1, 2, figsize=(12, 4))

# Plot ผลของ PCA
ax[0].scatter(images_PCA[:, 0], images_PCA[:, 1], c=labels, cmap='rainbow', alpha=0.5)
ax[0].set_aspect('equal', 'datalim')
ax[0].set(xlabel='PC1 score', ylabel='PC2 score')
ax[0].set_title('Data in the PCA-transformed space')

# Plot ผลของ UMAP
ax[1].scatter(images_UMAP[:, 0], images_UMAP[:, 1], c=labels, cmap='rainbow', alpha=0.5)
ax[1].set_aspect('equal', 'datalim')
ax[1].set(xlabel='Reduced dimension 1', ylabel='Reduced dimension 2')
ax[1].set_title('Data in the UMAP-transformed space')

# ใช้สีที่แตกต่างกันสำหรับแสดงจุดข้อมูลในสองมิติ จากคนละ class กัน (มี 10 classes จึงใช้ 10 สี)
fig.colorbar(sp, ax=ax, boundaries=np.arange(num_classes+1)-0.5).set_ticks(np.arange(num_classes))
plt.show()

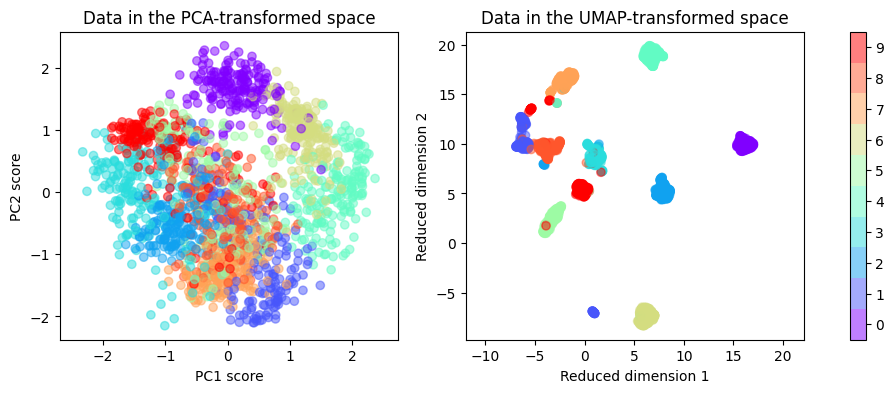
../../_images/b0a63fb1f9eac372050a0f4009df8cc2e89cb4fdb8dceab0ce29111c24e2e283.png

จะเห็นได้ว่าข้อมูลจากเทคนิค UMAP ส่งผลให้ข้อมูลจาก class เดียวกันเกาะกลุ่มกันได้ ในขณะที่ข้อมูลจากคนละ class (คนละสี) มีการกระจายตัวออกจากกันมากกว่าสิ่งที่ได้รับจาก PCA

ถึงแม้ว่าในตัวอย่างนี้ UMAP จะดูได้ผลที่ดีกว่า PCA แต่ก็ต้องรำลึกไว้เสมอว่าเทคนิคแต่ละเทคนิคก็มีข้อดี/ข้อเสีย และมีสมมติฐานที่แตกต่างกัน บางสถานการณ์อาจจะเหมาะกับเทคนิคประเภทนึงมากกว่าเทคนิคอีกประเภทนึง

เช่น

PCA เป็นเทคนิคที่มีสมมติฐานน้อยมาก และ PCA มักจะเอาข้อมูลที่ correlate กัน ยุบไปรวมกันอยู่บนมิติเดียวกัน ทำให้ PCA มักจะถูกนำไปใช้ในขั้นตอน preprocessing ก่อนที่จะเอาข้อมูลไปใช้วิเคราะห์ด้วยเทคนิคอื่น ๆ ต่อไป
เนื่องจาก PCA เป็นโมเดลแบบ linear ทำให้เราสามารถตีความข้อมูลได้ค่อนข้างง่ายกว่าเทคนิคที่เป็น nonlinear แต่ด้วยความเป็น linear เทคนิคนี้ก็จะไม่เหมาะสมกับข้อมูลที่มีความเป็น nonlinear สูงเช่นกัน
PCA วัดความห่างของข้อมูลด้วย Euclidean distance ถ้าหากเราต้องการวัดข้อมูลด้วย distance แบบอื่น PCA ก็จะไม่ค่อยเหมาะแล้ว อาจจะต้องไปใช้เทคนิคอื่น ๆ เช่น multi-dimensional scaling (MDS), Generalized MDS, t-SNE และ UMAP

ถ้าหากต้องการศึกษาเพิ่มเติมเกี่ยวกับเทคนิคเหล่านี้เป็นภาษาไทย สามารถเข้าไปดูได้ที่ MTEC machine learning mini-lecture: Session 2- Principals of unsupervised techniques ซึ่งเป็นส่วนนึงของ MTEC Machine Learning Workshop

ผู้จัดเตรียม code ใน tutorial: ดร. อิทธิ ฉัตรนันทเวช

Nonlinear Methods

Contents

Nonlinear Methods#

ตัวอย่างแรก#

ตัวอย่างที่ 2#

Nonlinear methods#